Trapping Rain Water II

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:

Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

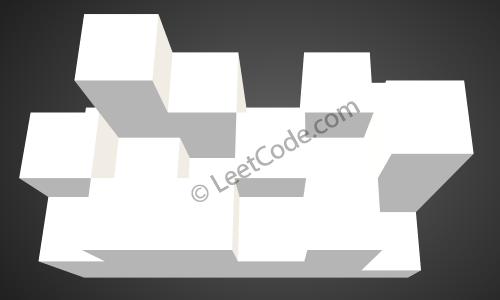
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

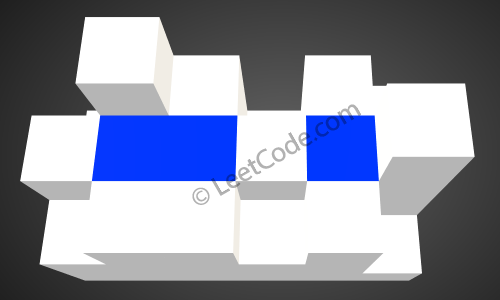
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.

Tips:

O(nmlog(n+m)) 建堆：O((2n+2m)log(2(n+m)))较少，可忽略

用PriorityQueue把选中的height排序。为走位，create class Cell {x,y, height}.

注意几个理论：

1. 从matrix四周开始考虑，发现matrix能Hold住的水，取决于height低的block。
2. 必须从外围开始考虑，因为水是被包裹在里面，外面至少需要现有一层。

以上两点就促使我们用min-heap: 也就是natural order的PriorityQueue.

process的时候，画个图也可以搞清楚，就是四个方向都走走，用curr cell的高度减去周围cell的高度。 若大于零，那么就有积水。

每个visited的cell都要mark. 去到4个方向的cell,加进queue里面继续process.

这里，有一点，和trapping water I 想法一样。刚刚从外围，只是能加到跟外围cell高度一致的水平面。往里面，很可能cell高度变化。

这里要附上curr cell 和 move-to cell的最大高度。

1. Same idea as the trap Rain Water I.
2. Since this is not 1-way run through a 1D array (2D array can go 4 directions...), need to mark visted spot.
3. Use PriorityQueue, sort lowest on top, because the lowest surroundings determines the best we can get.
4. Bukkit theory: the lowest bar determines the height of the bukkit water. So, we always process the lowest first.
5. Therefore, we use a min-heap, a natural order priorityqueue based on height.

6. Note: when adding a new block into the queue, comparing with the checked origin, we still want to add the higher height into queue. (The high bar will always exist and hold the bukkit.)

   Step:

   1. Create Cell (x,y,h)
   2. Priorityqueue on Cell of all 4 borders
   3. Process each element in queue, and add surrounding blocks into queue.
   4. Mark checked block

Code:

public class Solution {

    public class Cell {
        int row;
        int col;
        int height;
        public Cell(int row, int col, int height) {
            this.row = row;
            this.col = col;
            this.height = height;
        }
    }

    public int trapRainWater(int[][] heights) {
        if (heights == null || heights.length == 0 || heights[0].length == 0)
            return 0;

        PriorityQueue<Cell> queue = new PriorityQueue<>(1, new Comparator<Cell>(){
            public int compare(Cell a, Cell b) {
                return a.height - b.height;
            }
        });

        int m = heights.length;
        int n = heights[0].length;
        boolean[][] visited = new boolean[m][n];

        // Initially, add all the Cells which are on borders to the queue.
        for (int i = 0; i < m; i++) {
            visited[i][0] = true;
            visited[i][n - 1] = true;
            queue.offer(new Cell(i, 0, heights[i][0]));
            queue.offer(new Cell(i, n - 1, heights[i][n - 1]));
        }

        for (int i = 0; i < n; i++) {
            visited[0][i] = true;
            visited[m - 1][i] = true;
            queue.offer(new Cell(0, i, heights[0][i]));
            queue.offer(new Cell(m - 1, i, heights[m - 1][i]));
        }

        // from the borders, pick the shortest cell visited and check its neighbors:
        // if the neighbor is shorter, collect the water it can trap and update its height as its height plus the water trapped
       // add all its neighbors to the queue.
        int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int res = 0;
        while (!queue.isEmpty()) {
            Cell cell = queue.poll();
            for (int[] dir : dirs) {
                int row = cell.row + dir[0];
                int col = cell.col + dir[1];
                if (row >= 0 && row < m && col >= 0 && col < n && !visited[row][col]) {
                    visited[row][col] = true;
                    res += Math.max(0, cell.height - heights[row][col]);
                    queue.offer(new Cell(row, col, Math.max(heights[row][col], cell.height)));
                }
            }
        }

        return res;
    }
}